Rotary Positional Embeddings Explained

Introduction

The transformer architecture has seen a meteoric rise in its applications across various domains of machine learning. However, the architecture lacks an inherent understanding of the order or sequence of tokens. This necessitates some form of positional encoding, such as Rotary Positional Embedding (RoPE) [1]. This blog post delves into the mathematical formulation of RoPE and its practical implementation in PyTorch.

The Need for Positional Encodings

Transformers employ self-attention or cross-attention mechanisms that are agnostic to the order of tokens. This means the model perceives the input tokens as a set rather than a sequence. It thereby loses crucial information about the relationships between tokens based on their positions in the sequence. To mitigate this, positional encodings are utilized to embed information about the token positions directly into the model.

What is Rotary Positional Embedding (RoPE)?

RoPE is unique in that it encodes the absolute position $m\\$ of tokens through a rotation matrix $R_{\Theta, m}$, and also incorporates the explicit relative position dependency in the self-attention formulation. The idea is to embed the position of a token in a sequence by rotating queries and keys, with a different rotation at each position.

By rotating each query/key dependent on where they are in the sequence, we increasingly reduce the dot product (due to encouraging increasing levels of misalignment) depending on how far tokens are away from each other.

Mathematical Formulation in 2D

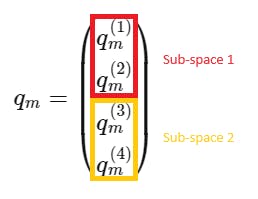
For a 2D query vector, $q_m = \begin{pmatrix} q_m^{(1)} \\ q_m^{(2)} \end{pmatrix}$, at a single position $m$, the rotation matrix $R_{\Theta, m}$ is a 2x2 matrix formulated as:

\[R_{\Theta,m} = \begin{pmatrix} cos⁡\ mθ & −sin⁡\ mθ \\ sin⁡\ mθ & cos⁡\ mθ \end{pmatrix}\]

where $\theta \in \mathbb{R}$ is a preset non-zero constant.

We can use this matrix to rotate a vector $q$, to obtain the new rotated vector $\hat{q}$:

$$\hat{q} = \left(\begin{array}{cc} \cos m \theta & -\sin m \theta \\ \sin m \theta & \cos m \theta \end{array}\right) \left(\begin{array}{l} q_m^{(1)} \\ q_m^{(2)} \end{array}\right)$$

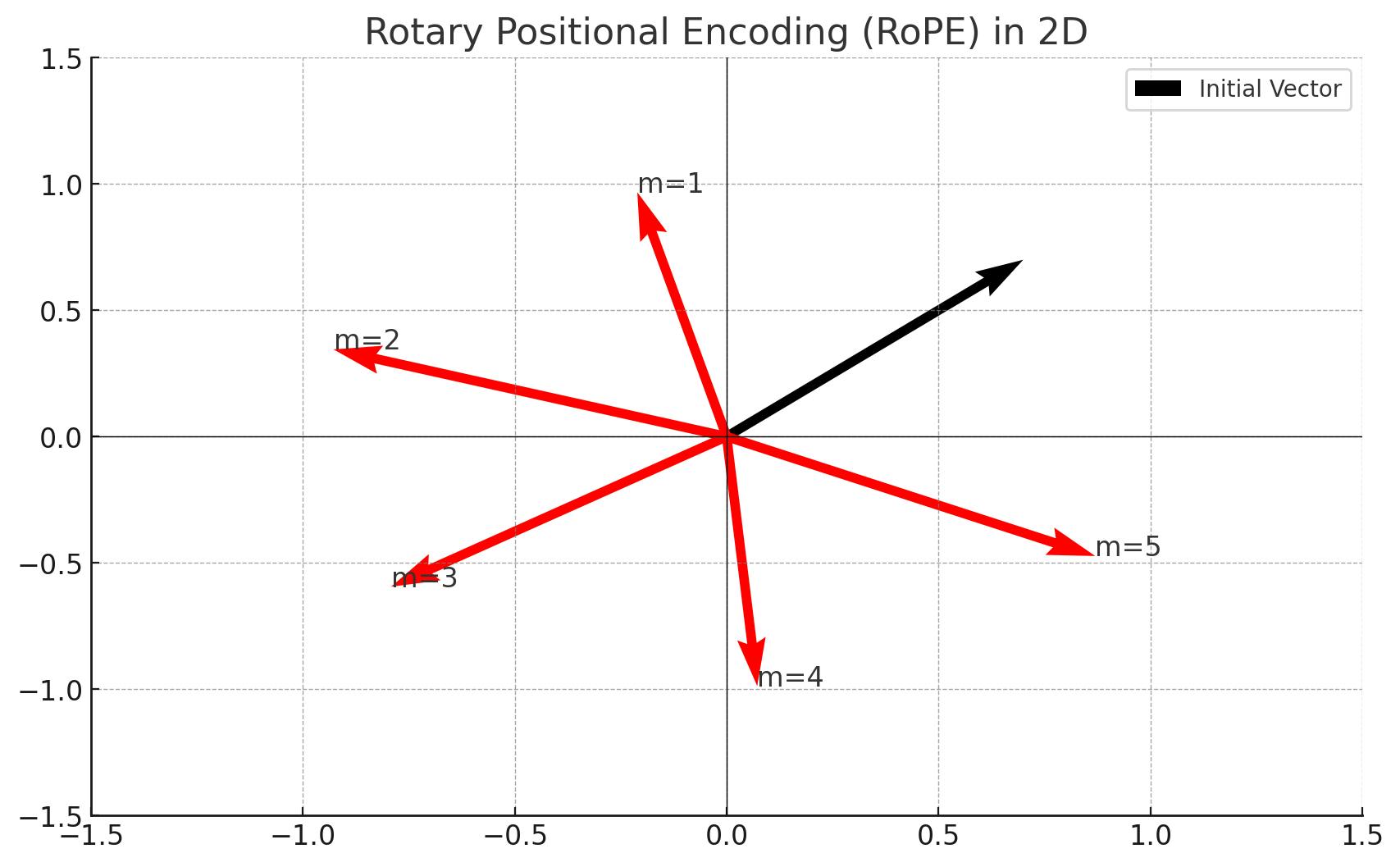
Here is a visualization of the rotation applied to the 2D vector $q$. The initial vector is displayed in black and the red vectors are the rotated versions of the initial vector.

General Mathematical Formulation

To generalize to any even dimension $d \ge 2$, we divide the $d$-dimensional space into $ \frac{d}{2}$ sub-spaces and apply rotations individually.

Let's see a simple example with $d=4$, the rotary matrix is defined as:

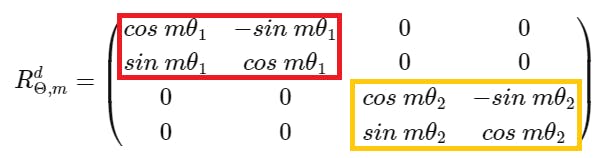
where $\Theta = \{\theta_i = 10000^{-2i/4}, i \in [1, 2]\}$ are the pre-defined parameters and $i$ the index for the $\frac{d}{2}$ sub-spaces, corresponding to:

The general form of the parameters is:
$\Theta = \{\theta_i = 10000^{-2(i -1) /d}, i \in [1, \dots, d/2]\}$

RoPE in Practice

In transformers, the rotation is applied to both queries and keys before the dot-product score is computed in the attention mechanism. For query $q_m$ in position $m$ and key $k_n$ in position $n$, the formula becomes:

\[q_m^T k_n = (R_{\theta,m}^d q_m )^T (R_{\theta,n}^d k_n ) = q_m^T R_{\theta,n-m}^d k_n,\]

where $R_{\theta,n-m} = (R_{\theta,m}^d)^T R_{\theta,n}^d $ .

Python Implementation of Rotary Matrix

def get_rotary_matrix(context_len: int, embedding_dim: int) -> torch.Tensor:
    """
    Generate the Rotary Matrix for ROPE

    Args:
        context_len (int): context len
        embedding_dim (int): embedding dim

    Returns:
        torch.Tensor: the rotary matrix of dimension context_len x embedding_dim x embedding_dim
    """
    R = torch.zeros((context_len, embedding_dim, embedding_dim), requires_grad=False)
    positions = torch.arange(1, context_len+1).unsqueeze(1)
    # Create matrix theta (shape: context_len  x embedding_dim // 2)
    slice_i = torch.arange(0, embedding_dim // 2)
    theta = 10000. ** (-2.0 * (slice_i.float()) / embedding_dim) 
    m_theta = positions * theta
    # Create sin and cos values
    cos_values = torch.cos(m_theta)
    sin_values = torch.sin(m_theta)
    # Populate the rotary matrix R using 2D slicing
    R[:, 2*slice_i, 2*slice_i] = cos_values
    R[:, 2*slice_i, 2*slice_i+1] = -sin_values
    R[:, 2*slice_i+1, 2*slice_i] = sin_values
    R[:, 2*slice_i+1, 2*slice_i+1] = cos_values
    return R

# ... Init parameters and random input
batch_size = 16
context_len = 128
embedding_dim = 1024
ff_q = nn.Linear(embedding_dim, embedding_dim, bias=False)
ff_k = nn.Linear(embedding_dim, embedding_dim, bias=False)
x = torch.randn((batch_size, context_len, embedding_dim))

# ... In the attention computation
queries = ff_q(x)
keys = ff_k(x)

R_matrix = get_rotary_matrix(context_len, embedding_dim)
queries_rot = (queries.transpose(0,1) @ R_matrix).transpose(0,1)
keys_rot = (keys.transpose(0,1) @ R_matrix).transpose(0,1)

# ... Compute the score in the attention mechanism using the rotated queries and keys

Explanation of Components

Initialization: We initialize a 3D tensor (R) to store the rotary matrices for each position $m$.
```
 R = torch.zeros((context_len, embedding_dim, embedding_dim), requires_grad=False)
```
Positional and Dimensional Slicing: We create a tensor of positions and another tensor slice_i for indexing into our $d$-dimensional space.
```
 positions = torch.arange(1, context_len+1).unsqueeze(1)
 slice_i = torch.arange(0, embedding_dim // 2)
```
Theta Calculation: A decay factor $\theta$ is calculated, which scales down the effect of positions for higher dimensions.
```
 theta = 10000. ** (-2.0 * (slice_i.float()) / embedding_dim) 
 m_theta = positions * theta
```
Sin and Cos Values: We calculate the sine and cosine values for each $m\theta$.
```
 cos_values = torch.cos(m_theta)
 sin_values = torch.sin(m_theta)
```

Populating (R): We use slicing to populate the rotary matrix efficiently.

 R[:, 2*slice_i, 2*slice_i] = cos_values
 R[:, 2*slice_i, 2*slice_i+1] = -sin_values
 R[:, 2*slice_i+1, 2*slice_i] = sin_values
 R[:, 2*slice_i+1, 2*slice_i+1] = cos_values

Rotate the queries and keys: Apply the rotary matrix to the queries and keys inside the attention computation.

 R_matrix = get_rotary_matrix(context_len, embedding_dim)
 queries_rot = (queries.transpose(0,1) @ R_matrix).transpose(0,1)
 keys_rot = (keys.transpose(0,1) @ R_matrix).transpose(0,1)

References

[1] Roformer: Enhanced transformer with rotary position embedding, Jianlin Su et al., 2021.

After Hours Research